When Am I Ever Going to Use Math after High School?
- Dianne McKinley
- Mar 3, 2023
- 7 min read
Updated: Jan 8

I know when I was in the classroom I had the infamous poster below up in my classroom. Students are always asking the question “When Am I Ever Going to Use This?” What I am realizing now is they are asking this because, as math teachers, we are NOT doing enough to make sure that question is answered BEFORE they ask it. Math teachers, much like I was when I was in the classroom, have so many standards to cover for their course or grade level, they do not feel like they have time to show students the connections that must be made between what we are teaching and how it will be used and applied. The reality is teachers must make those connections and use the math they are teaching in context if they want their students to truly learn and understand the math they are teaching.

Higher Order Thinking Skills
Lately, I have been presenting professional development sessions on Higher Order Thinking Skills. One of the questions I ask participants is; “What is the difference between Facts and Knowledge?” The basic explanation of “Facts” are objective pieces of information that can be proven to be true, while “Knowledge” is the accumulation of Information, techniques, and the skills to apply and use them. As math teachers we have the art of teaching facts down quite well. We are falling short on making sure our students are knowledgeable.
Just teaching students a bunch of facts is something that many of them can already do using Google. If we do not answer the question; “When Am I Ever Going to Use This?” it does not help the students become knowledgeable! If the connections are not made and no reason is shown to retain the information being taught, then we are just sharing facts which may or, more likely, may not be remembered.
Granted all the connections may not be earth shattering, but they still MUST be made. A good example of this would be some of the key SAT Assessment Algebra skills like the Distributive Property, Difference of Two Squares, and the Square of a Binomial/Perfect Square Trinomial. Math teachers usually know what you are talking about when you mention these three concepts, especially the Distributive Property but not always the other two. If you would ask the average person what the Square of a Binomial is, more than likely they will not know what you are talking about and even more likely they would not remember the pattern it involves.
SAT Assessment Algebra Examples

The Square of a Binomial is ( a + b )2 = a2 + 2ab + b2 or ( a – b )2 = a2 – 2ab + b2. That may or may not ring a bell for you. But what if I showed you how “You might actually use this (outside of math class).” Take for instance if you had to calculate 342 and you didn’t have a calculator handy (or even if you do have a calculator handy it is easier to do mentally than using a calculator) Most people would write down 34 x 34 and use the standard algorithm to do the calculations. If you are truly knowledgeable about the Square of a Binomial and know how to use and apply it, you would just write down 900 + 240 + 16 and get 11156. Most people see where the 900 comes from. They also see where the 16 comes from. The 240 totally confuses them. If you treat 342 as ( 30 + 4 )2 and understand the fact that is stated at the start of this paragraph you will see where the 240 comes from. It is the 2 x 30 x 4 Once you practice this a couple of times and I ask you to calculate 452 you would quickly write 1600 + 400 + 25 and get 2025. You try it now. What is 672? Did you easily get 4489?
In similar fashion do we show students that multiplying problems like 7 x 47 can be easily done by splitting 47 up into ( 40 + 7 ) and using the Distributive Property? Most students can easily calculate 7 x 40 in their heads, 280. Most students can easily calculate 7 x 7 in their heads, 49. With a little practice students can add 280 + 49 in their heads to get 329. Do you show your students how they might use the Distributive Property outside of math class? If you do, you will be surprised how much longer they will remember that important skill. Once students do see it they can easily multiply weird numbers like 7 x 83. 560 + 21 to get 581 in their heads without a calculator. You try it. What is 8 x 54?
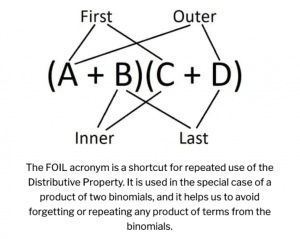
After you have shown students this, you have beautifully set up the next step up in the progression. Ask students to multiply 72 x 29. Would they understand how the problem was worked, if you wrote 1400 + 630 + 40 + 18 to get 2088 on the board? Show students this and see if they understand how it works now that they have seen how the distributive property can be applied and used. Try it. You will be surprised how well students understand math when you give them the reasons why they can actually use the math they are learning.
Financial Literacy
Moving on to higher math classes. Currently all 8th graders and 12th graders have financial literacy standards that are supposed to be covered before they enter high school and before they graduate but there is not an official course where all the standards must be taught (as of yet.) There is a large ground swell and a proposed Indiana Senate Bill for students to take a “Financial Literacy” course to graduate from high school. This is because students have been taught the math they need to understand all the information required for a financial literacy course but have not necessarily been shown how they will use or apply those math concepts to help them have financial literacy skills.
One of the strands in Algebra 2 is specifically about Exponential and Logarithmic Equations and Functions. When I talk to Algebra 2 teachers they do not like to get into Monthly Mortgage Payments and Amortizations Schedules because they think or say they are too complicated for the math concepts being taught in the Algebra 2 course. Actually it is just the opposite. Monthly Mortgage Payments and Amortizations Schedules show exactly how exponential functions work and put all the skills the students learn about exponential functions into application and use. Students are very capable of doing complex math problems if there is interest and application. Buying a car, home or making purchases are extremely interesting concepts to high school students.

Given a Calculator and the Numbers to Enter This is a relatively easy problem.
Real-World Problems
Matter of fact if you look at Algebra 2 standards AII.EL.6 it says “Represent real-world problems using exponential and logarithmic functions and solve such problems with technology. Interpret the solutions and determine whether they are reasonable.” That can be done easily using the FREE Excel Downloads of Mortgage Loan Calculators and Amortization Schedules. Having students look up current mortgage interest rates (30 Year Fixed – approximately 7% – 8% and 15 Year Fixed – approximately 6.5% – 7%) then using either the actual exponential formulas or the Excel spreadsheet compare the differences .1% interest rate makes to monthly payments or the difference between a 15 year loan and a 30 year loan monthly payment. My students were always surprised to find that it was not double and how much interest they saved by going with a 15 year loan.
We spent another day talking about credit cards and how they use exponential functions for their calculations. Very few students, and I would venture to say that very few adults today, have a good grasp on credit cards and how the interest and minimum payments really work. Store credit cards are the absolute worst. Test your skills. Do you know what the Macy’s Credit Card Annual Percentage Interest Rates are currently? 15% – 20% – 25% – 30% – Above 30%, which is correct? If you said Above 30% you would be correct. Surprised? Take a look at the current Macy’s Credit Card Disclosure Statement. I have had both students and parents comment that the lessons we did on home loan and credit card payments were some of the most valuable and important lessons that the students were taught. When I would see students in the community years later, they would comment about the lessons we did around loans. It was very enlightening for them and made the math I was teaching very real for them.
Conclusion
Overall, making sure that students understand the math you are teaching them and know how it will be used in life after high school is imperative for students. Just giving students a bunch of facts and information so you can say or check off the list of standards that you covered throughout the year is a disservice to both your students and the subject you are teaching. True knowledge is all about being able to understand, apply, and use the concepts being taught. If all we are doing is teaching facts where the students have to ask “When Am I Ever Going to Use This?” we might as well be teaching our students how to Google! I can and do regularly Google facts and information I need or just want to know. We owe it to our students not to just turn them into human Google devices just knowing a bunch of facts. If we are truly doing what is best for our students we will be making sure that not only do they know the facts but also how those facts are applied and used. That is when we can say we have knowledgeable students!
How are you going to ensure your students know and understand the question: “When Am I Ever Going to Use This?”





